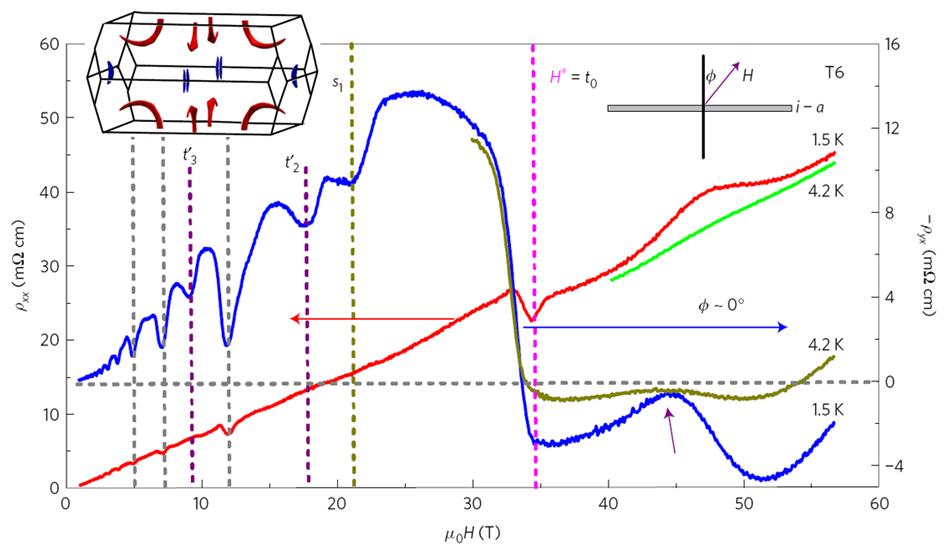
High magnetic field study of TaP up to 58 T,rxxandryxversus magnetic fieldHat 1.5 K and 4.2 K (data in selected field range). The inset shows the locations of the two weyl nodes W1 and W2 in the projectedkx–kyplane in momentum space.
(Nature Physics (2017) doi: 10.1038/nphys4183)
Background
The recently discovered topological Weyl semimetals in the TaAs family open up a new territory. In contrast to a conventional metal/semimetal, the metallicity of a Weyl semimetal is guaranteed by the presence of Weyl nodes. Weyl nodes are topological objects in three-dimensional metals. In the presence of translational symmetry, they cannot be removed unless pairs of Weyl nodes of opposite chirality are moved together to annihilate each other. Thus, the Weyl node annihilation is a unique topological phenomenon associated with Weyl fermions.
What we discover?
In the Weyl semimetal TaP, which possesses two types of Weyl nodes (four pairs of W1 and eight pairs of W2 nodes), we observed such a magnetic coupling between the electron pockets arising from the W1 Weyl fermions. As a result, their lowest Landau bands move above the chemical potential, leading to a sharp sign reversal in the Hall resistivity at a specific magnetic field corresponding to the separation in momentum space of the W1 Weyl nodes. These findings reveal the nontrivial topology of Weyl fermions in high-field transport measurements and demonstrate the observation of Weyl node annihilation.
Why is this important?
The magnetic tunnelling of the lowest Landau band (LLB) has never been observed because, in the few existing semimetals where LLBs can be accessed (for example, bismuth and graphite), the pockets are far separated inkspace so that magnetic tunnelling is negligibly small. Here, we report the observation of magnetic tunnelling of the LLBs in any material irrespective of its topological nature. Furthermore,we show that the magnetic tunnelling of the LLBs in TaP reveal the nontrivial topology of Weyl fermions in high-field measurements.
Why did they need WHMFC?
The ultra-quantum limit refers to a condition where, at a sufficiently high magnetic field, all higher Landau bands are pushed away from the Fermi level whereas only the lowest Landau band crosses the chemical potential. Understanding their properties of Weyl semimetals beyond the ultra-quantum limit has been a fertile ground for discovering new physics. Whereas the energy of the lowest Landau band of a conventional Fermi pocket increases with magnetic field due to the zero-point energy, the lowest Landau band of Weyl cones stays at zero energy unless a strong magnetic field couples Weyl fermions of opposite chirality.
Who did the research?
Cheng-Long Zhang1, Su-Yang Xu2, C. M.Wang3,4, Ziquan Lin5, Z. Z. Du3,6, Cheng Guo1,Chi-Cheng Lee7,8, Hong Lu1, Yiyang Feng1, Shin-Ming Huang9, Guoqing Chang7,8, Chuang-Han Hsu7,8, Haiwen Liu1, Hsin Lin7,8, Liang Li5, Chi Zhang1,10, Jinglei Zhang11,12, Xin-Cheng Xie1,10, Titus Neupert13, M. Zahid Hasan2, Hai-Zhou Lu3*, JunfengWang5* and Shuang Jia1,10*
1International Center for Quantum Materials, School of Physics, Peking University, China.
2Laboratory for Topological Quantum Matter and Spectroscopy (B7), Department of Physics, Princeton University, Princeton, New Jersey 08544, USA.
3Institute for Quantum Science and Engineering and Department of Physics, South University of Science and Technology of China, Shenzhen 518055, China.
4School of Physics and Electrical Engineering, Anyang Normal University, Anyang 455000, China.
5Wuhan National High Magnetic Field Center, Huazhong University of Science and Technology, Wuhan 430074, China.
6School of Physics, Southeast University, Nanjing 211189, China.
7Centre for Advanced 2D Materials and Graphene Research Centre National University of Singapore, 6 Science Drive 2, Singapore 117546, Singapore.
8Department of Physics, National University of Singapore, 2 Science Drive 3, Singapore 117542, Singapore.
9Department of Physics, National Sun Yat-Sen University, Kaohsiung 804, Taiwan.
10Collaborative Innovation Center of Quantum Matter, Beijing 100871, China.
11High Magnetic Field Laboratory, Chinese Academy of Sciences, Hefei 230031, Anhui, China.
12Hefei Science Center, Chinese Academy of Sciences, Hefei 230031, Anhui, China.
13Department of Physics, University of Zurich, 190, CH-8052, Winterthurerstrass, Switzerland.
