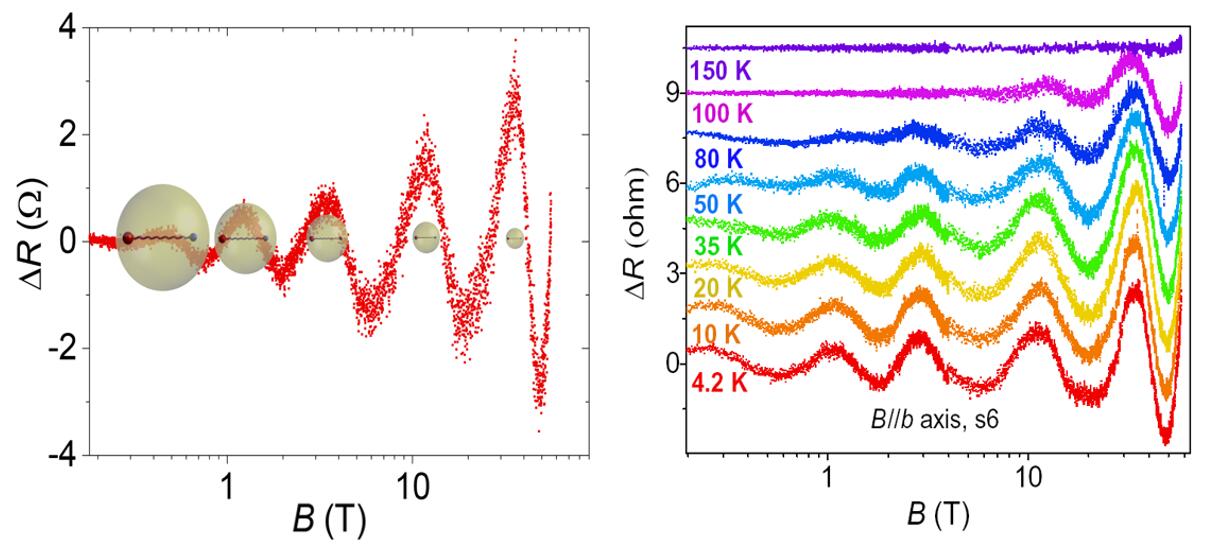
Left: Log-periodic quantum oscillations in ZrTe5.
Right: Temperature dependence of the log-periodic oscillations for sample s6.
(Science advances 4:eaau5096, 2018, http://advances.sciencemag.org/content/4/11/eaau5096)
To date, researchers have observed quantum oscillations in diverse materials, which can be classified into two classes: one is quantum oscillations with a periodicity in 1/B, for example, the Shubnikov-de Haas oscillations in magnetoresistance arising from Landau quantization. The other is periodic in B, originating from the quasi-particle quantum interference in mesoscopic systems, such as the Aharonov–Bohm and Altshuler-Aronov-Spivak oscillations in ring or cylinder structures in magnetoresistance. Each type of quantum oscillation reflects an important underlying physical mechanism and corresponds to new physical laws.
What did scientists discover?
Scientists discovered a new log-periodic quantum oscillation in high-quality single-crystal ZrTe5, a three-dimensional layered topological material. Under a strong magnetic field, transport carriers of the topological material enter the lowest Landau level, the so-called quantum limit. The research team used a 65 T pulsed field magnet and discovered log-periodic oscillations in magnetoresistance beyond the quantum limit of ZrTe5. This novel discovery is further confirmed by the magnetotransport results from different samples and different facilities with the maximum magnetic field up to 58 Tesla. This log-periodic oscillations cannot be attributed to conventional two types of quantum oscillations, and points to a new quantum state beyond the quantum limit.
Why is this important?
Log-periodic quantum oscillation is discovered for the first time in a solid-state system. This discovery represents the third known class of quantum oscillations after a nearly 90 year history of quantum oscillation measurements. Analyses reveal that the novel log-periodicity of the oscillating structures in the magnetoresistance demonstrates the existence of discrete scale invariance (DSI). In quantum systems, the best-known system with DSI is the Efimov trimer bound state, which has been observed in cold atom experiments and has inspired a growing research interest in related fields. Scientists further reveal that log-periodic quantum oscillation is a universal behavior in Dirac or topological materials. This provides a new experimental tool for exploring novel relativistic quantum phenomenon beyond condensed matter physics.
Why did they need WHMFC?
In a steady field, scientist only observed two or three quantum oscillations in ZrTe5. In a pulsed high magnetic field, they discovered oscillations involving up to five oscillating cycles (5 peaks and 5 dips), giving a strong evidence of the log-periodicity of the quantum oscillations.
Who did the research?
Prof. Jian Wang, Prof. X. C. Xie at Peking University are corresponding authors of this work. Prof. Junfeng Wang and Prof. Liang Li at Wuhan National High Magnetic Field Center, Prof. Jiaqiang Yan and Prof. David Mandrus at Oak Ridge National Laboratory, Prof. Yong Wang at Zhejiang University and Prof. Jiyan Dai at The Hong Kong Polytechnic University collaborated on this project. Details of all co-authors please find in the full-length publication:
http://advances.sciencemag.org/content/4/11/eaau5096
Funding
This work was supported by the National Basic Research Program of China, the National Natural Science Foundation of China, the Open Project Program of the Pulsed High Magnetic Field Facility, the Key Research Program of the Chinese Academy of Sciences, the US Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division, the Gordon and Betty Moore Foundation’s EPiQS Initiative and the Postdoctoral Fellowships Scheme of the Hong Kong Polytechnic etc.
