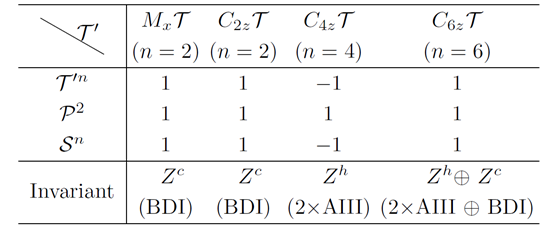
Figure 1: The topological classification of the 1D gapped superconducting systems with the Local Magnetic Symmetries.

Figure 2: (a) A C_4zT-preserving superconducting wire aligned along z direction. (b) The topological phase diagram. (c)the spectrum of nontrivial phase with an open boundary on both sides, in which four MZMs appear at zero energy.

Background

Topological superconductors (TSCs) are new kind of topological quantum states with fully superconducting gapped band structure in the bulk, but support gapless excitations called Majorana zero modes (MZMs) at the boundaries. Because of their nonlocal correlation and non-Abelian statistic nature, MZMs are proposed as the qubits of topological quantum computation.

To identify a TSC, one should first ascertain its topological classification. Without the consideration of crystalline symmetries, the Bogoliubov-deGennes (BdG) Hamiltonians of the 1D superconductors only have the Z₂ classification. The mirror reflection symmetry and rotational symmetries can enrich the classification to Z class with multiple MZMs. Nevertheless, the topological classification of superconductors with general magnetic symmetries is still an open question.

What we discover?

We proposed the method to classify the 1D topological superconducting phase by examining the compatibility between different MZMs. Then we analyzed the topological classification of gapped superconducting wires with local magnetic symmetries (LMSs),in which the time-reversal symmetry is broken but its combinations with certain crystalline symmetries, such as M_xT, C_2zT, C_4zT, and C_6zT, are preserved. These operators do not change the position of electrons. Hence, they act on the BdG Hamiltonian like time-reversal operator.The M_xT and C_2zT cases are equivalent to the BDI class with chiral topological invariant Z^c. While C_4zT case is characterized by the helical Z^hinvariant, which indicates that Z-pairs of MZMs could exist at the end of the superconducting wire. In the C_6zT case, the topology of the whole BdG Hamiltonian is classified by Z^h+Z^c. In such a novel topological phase, the helical and chiral MZMs can coexist.The minimal models preserving C_4zT symmetry are constructed to illustrate their novel topological properties.

Why is this important?

The helical and chiral MZMs coexisting TSCs provide the new platform to manipulate the MZMs. Furthermore, these novel TSC phases not only enrich the variety of the 1D TSC, but also provide luxuriant building blocks for the construction of new type 2D and 3D TSCs. For example, one can couple the 1D TSCs in y direction to construct a 2D TSC. The high symmetry lines k_y= 0 and k_y=pi in momentum space preserve the 1D LMS. With proper parameters, the k_y= 0 and k_y=pi lines can belong to distinct topological phase, and result in the gapless propagating Majorana edge states connecting the conducting bands and valence bands.

Who did the research?

Jinyu Zou¹, Qing Xie¹, Zhida Song²and Gang Xu^1*

¹Wuhan National High Magnetic Field Center & School of Physics,

Huazhong University of Science and Technology, Wuhan 430074, China

²Department of Physics, Princeton University, Princeton, New Jersey 08544, USA

*e-mail:gangxu@hust.edu.cn

Acknowledgements

We thank Chaoxing Liu for valuable discussion. This work is supported by the Ministry of Science and Technology of China (No. 2018YFA0307000) and the National Natural Science Foundation of China (No. 11874022).

Natl Sci Rev, nwaa169 (2020), DOI:https://doi.org/10.1093/nsr/nwaa169